Literature Review
Literature Review, Concepts and Resources
Jaccard Index
The Jaccard similarity coefficient is a measure of similarity for two sets. The formula for the index is (size of intersection of two sets)/(size of union), so the index can take any value from 0 to 1.
Collaborative Filtering
Collaborative filtering is a way to filter information or create recommendations based on patterns and recommendations from other agents. In other words, it is a method of creating customized recommendation with information from other users.
Matrix Factorization
In linear algebra, Matrix Factorization is the decomposition of a matrix into a product of matrices.
In the practice of recommender systems, is a method of collaborative filtering. MF can help find latent features that influence the interaction between users and items. Since there’s an assumption that these factors/ features are fewer than the observations (user-item), MF is recruited to lower the dimensionality of data , with the purpose of lowering the dimensionality of data. MF can be helpful in finding latent features that influence the interation between users and items.
As for the mathematics behind MF: If the number of users is $U$, and the number of items is $I$, $M$ is the initial matrix with the preferences of users regarding the items, then the size of $M$ is $U \times I$.
To find $F$ features, the two matrices that will be created from $M$ are $Q$ and $R$, with sizes $U \times F$ and $I \times F$, so that the product of $Q$ and $R^{T}$ is $M$.
Single Value Decomposition
If we’re looking to decompose an $m \times n$ matrix $M$, then through SVD it will be decomposed into 3 different matrices, as $M = U S V^{H}$, where:
1) $U$ : $m \times n$ unitary matrix, whose columns are called the left singular vectors of matrix $M$, and a set of orthonormal eigenvectors of $MM^{H}$ (where $M^{H}$: conjugate transpose of the $M$) 2) $S$ : $m \times n$ diagonal matrix with non-negative cells, whose diagonal values are known as the singular values of $M$, and also the square roots of the non-zero eigenvalues of both $M^{H} M$ and $MM^{H}$. 3) $V$: $n \times n$ unitary matrix, whose columns are the right singular vectors of $M$, and orthonormal eigenvector of $M^{H} M$.
More information about SVD and its applications on Filtering can be found in the following paper: Vozalis, Manolis G., and Konstantinos G. Margaritis. “Applying SVD on Generalized Item-based Filtering.” IJCSA 3.3 (2006): 27-51.
Neural Collaborative Filtering
He, Xiangnan, et al. “Neural collaborative filtering.” Proceedings of the 26th International Conference on World Wide Web. International World Wide Web Conferences Steering Committee, 2017.
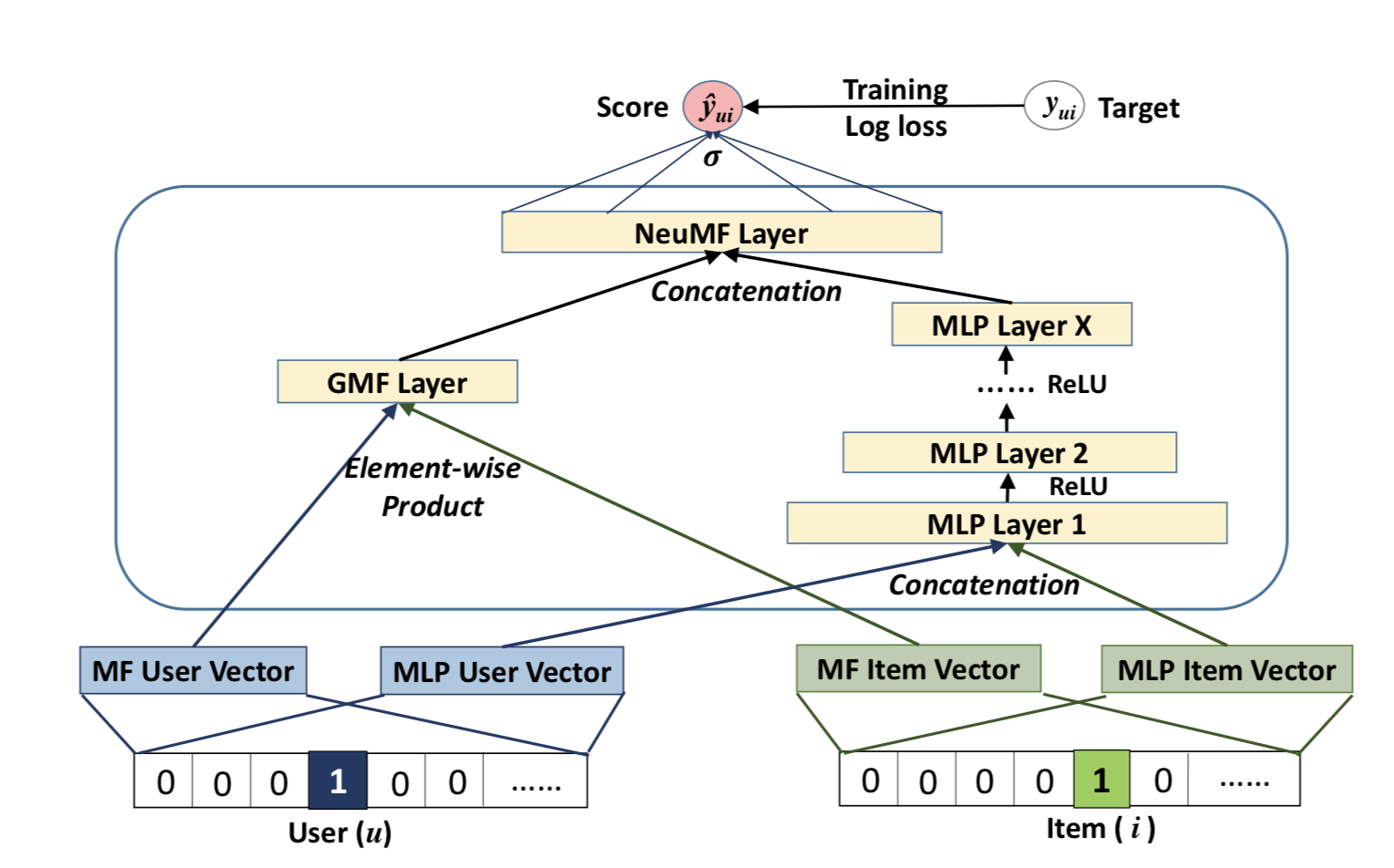
As we see from the architectural image, NCF creates vectors for multi-layer peceptron (MLP) and matrix factorization (MF) for both the user and the item. Both MF and MLP are performed in order to project data of higher dimensions to a lower dimension. Then the products of MF and MLP are combined through Neural MF to make the final prediction.
Principal Component Analysis (PCA)
A technique used to reduce the dimensionality of the feature space and find the directions of most variation in a data set. It is a useful approach for feature selection and for avoiding the curse of dimensionality. Performing a PCA is just finding the eigenvalues and eigenvectors of the data set’s correlation matrix, $Σ=Y^TY$, where $Y=X−μX$. $X$ is an $N×M$ matrix of data points, where each row is one of the N samples and each column in one of the M features, and $μX$ is the empirical mean value of the data set.
k-NN algorithm
The k-nearest neighbors algorithm (k-NN) is a non-parametric method used for classification and regression. In both cases, the input consists of the k closest training examples in the feature space. The output depends on whether k-NN is used for classification or regression; i.e. in k-NN classification, the output is a class membership whereas in k-NN regression, the output is the property value for the object.
k-means clustering
k-means clustering is a method popular of vector quantization that is popular for cluster analysis in data mining. This algorithm aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean, serving as the center of the cluster, also known as the centroid.